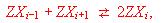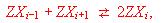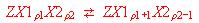Particle-Distribution in a Microporous Material
Andreas Kunzmann, Roland Seifert and Gion Calzaferri
Department of Chemistry and Biochemistry, University of Bern, Freiestrasse 3,
CH-3000 Bern 9, Switzerland
Abstract
Equilibria in zeolites and other microporous materials are discussed. We
present an independent particles in a box approach, which leads to a
thermodynamic description of internal occupation equilibria of the type
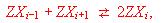
where Z denotes the framework of the material and X the particles that
can interchange places. The independent particles in a box are defined
by considering a crystal consisting of a finite number of unit cells or
boxes each of which can be filled with a specific number of particles.
All empty sites in a box have equal probability to be occupied,
independent of the number of particles present, as long as sites are
available. Each time a particle does fall in a box, the probability for
a next one to hit this box is reduced by one divided by the number of
sites available in an empty box. Hence, as soon as a box is filled, the
probability for a particle to hit it becomes zero. The maximum number of
particles in the system is equal to the maximum number of sites in a
box, multiplied by the number of boxes. This allows equilibrium
constants and the decrease of entropy as a function of the equivalent
fraction of exchanging species to be calculated. We show that the plot
of the logarithm of the equilibrium constant versus the equivalent
fraction of exchanging species is not linear, and that the non-linearity
is caused by the decrease of entropy. Based on this observation we
suggest the independent particles in a box to be used as a reference for
"ideal behaviour" and to serve as a reference for determining activity
coefficients. The generalisation of the theory leads to the independent
particles in boxes with different sites. It is discussed in detail with
regard to two non-equivalent sites corresponding to the internal
equilibria
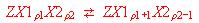
in which X1 and X2 are the same species but occupy site 1 and
2, respectively, of a box. We show the solution of this problem and
explain the distribution of the particles among the different sites, as
a function of the average exchange degree.
Download Mathcad file
partiv2.mcd
published in: J. Phys. Chem. B 1999, 103, 18.